By monitoring correlated time discrepancy between two spatially-separated clocks one could search for passage of topological defects (TD), such as domain wall pictured here. Domain wall moves at galactic speeds ~ 300 km/s. Here the clocks are assumed to be identical. Before the TD arrival at the first clock, the apparent time difference is zero, as the clocks are synchronized. As the TD passes the first clock, it runs faster (or slower, depending on the TD-SM coupling), with the clock time difference reaching the maximum value. Time difference stays at that level while the defect travels between the two clocks. Finally, as the defect sweeps through the second clock, the phase difference vanishes. For intercontinental scale network, l~ 10,000 km, the characteristic time 30 seconds.

Despite solid observational evidence for the existence of dark matter, its nature remains a mystery. A large and ambitious research program in particle physics assumes that dark matter is composed of heavy-particle-like matter. That community hopes to see events of dark matter particles scattering off individual nuclei. Considering nil results of the latest particle detector experiments (see excellent discussion here), this assumption may not hold true, and significant interest exists to alternatives.

Now what about atomic clocks? Atomic clocks are arguably the most accurate scientific instruments ever build. Modern clocks approach the 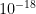fractional inaccuracy, which translates into astonishing timepieces guaranteed to keep time within a second over the age of the Universe. Attaining this accuracy requires that the quantum oscillator be well protected from environmental noise and perturbations well controlled and characterized. This opens intriguing prospects of using clocks to study subtle effects, and it is natural to ask if such accuracy can be harnessed for dark matter searches.

Posing and answering this question is the subject of our recent paper:
Hunting for topological dark matter with atomic clocks, A. Derevianko and M. Pospelov, arXiv:1311.1244.

We consider one of alternatives to heavy-particle dark matter and focus on so-called topological dark matter. The argument is that depending on the initial quantum field configuration at early cosmological times, light fields could lead to dark matter via coherent oscillations around the minimum of their potential, and/or form non-trivial stable field configurations in space (topological defects). The stability of this type of dark matter can be dictated by topological reasons.

I know, this sounds a little bit too far fetched to an atomic physicist. Well, ferro-magnets could serve as a familiar analogy. Here topological defects are domain walls separating domains of well-defined magnetization. Above the Curie point, the sample is uniform, but as the temperature is lowered, the domains start to form. So one could argue that as the Universe was cooling down after the Big Bang, quantum fields underwent a similar phase transition.

Generically, one could talk about 0D topological defects (=monopoles), 1D=strings, and 2D=walls. Dark matter would form out of such defects. The light masses of fields forming the defects could lead to a large, macroscopic, size for a defect. Based on observations and simulations, astronomers have a good idea of how dark matter moves around the Solar system. The defects would fly through the Earth at galactic velocities ~ 300 km/s. Now if the defects couple (non-gravitationally) to ordinary matter, one could think of a detection scheme using sensitive listening devices, e.g., atomic clocks. In fact one would benefit from a network of clocks, as one would cross-correlate events occurring at different locations.

Phenomenologically, the dark matter interaction with ordinary matter could be described as a transient variation of fundamental constants. The coupling would shift atomic frequencies and thus affect time readings. During the encounter with a topological defect, as it sweeps through the network, initially synchronized clocks will become desynchronized. This is illustrated in the figure.

The real advantage of clocks is that these are ubiquitous. Several networks of atomic clocks are already operational. Perhaps the most well known are Rb and Cs atomic clocks on-board satellites of the Global Positioning System (GPS) and other satellite navigation systems. Currently there are about 30 satellites in the GPS constellation orbiting the Earth with an orbital radius of 26,600 km with a half of a sidereal day period. As defects sweep through the GPS constellation, satellite clock readings are affected. For two diametrically-opposed satellites the maximum time delay between clock perturbations would be ~ 200 s, assuming the sweep with a typical speed of 300 km/s. Different types of topological defects (e.g., domain walls versus monopoles) would yield distinct cross-correlation signatures. While the GPS is affected by a multitude of systematic effects, e.g., solar flares, temperature and clock frequency modulations as the satellites come in out of the Earth shadow, none of conventional effects would propagate with 300 km/s through the network. Additional constraints can come from analyzing extensive terrestrial network of atomic clocks on GPS tracking stations.

The performance of GPS on-board clocks is certainly lagging behind state-of-the art laboratory clocks. Focusing on laboratory clocks, one could carry out a dark matter search employing the vast network of atomic clocks at national standards laboratories used for evaluating the TAI timescale. Moreover, several elements of high-quality optical links for clock comparisons have been already demonstrated in Europe, with 920 km link connecting two laboratories in Germany.

Naturally I hope that this proposal motivates dark matter searches with atomic physics tools pushing our “listening capabilities” to the next level. This proposal could provide fundamental physics motivation to building high-quality terrestrial and space-based networks of clocks. As the detection schemes would benefit from improved accuracy of short-term time and frequency determination, following this path could stimulate advances in ultra-stable atomic clocks and Heisenberg-limited time-keeping.